Adding the CCC to Your Curriculum
Cross-Cutting Concepts (CCC’s) lend a sharper focus to the other two dimensions. Each CCC presents a unique lens in which to focus upon the content while the practice provides the method in which the content is explored. The particular focus of “Scale, Proportion, and Quantity” is best described in the words of the Framework below.
To begin the process of adding a pattern focus to your curriculum, begin with one activity or lesson. For example, Analyzing & Interpreting Data Activity #3: Most Average Person does not need to be altered in order to apply the third dimension of CCC’s. Identifying scale, proportion, and quantity between people within the activity sharpens the focus of the activity and provides touchstones for students throughout discourse. Framing questions around scale, proportion, and quantity will provide structure for discourse, notebooking, and student thinking. Students are exploring the activity (content in this case) by way of analyzing and interpreting data (practice). The activity is sharpened and focused through the lens of scale, proportion, and quantity (CCC). In this way, the activity has not been drastically altered. It has rather been more focused for both students and teachers in communication, analyzation, and discourse.
After initial implementation, instructors will be able to identify other areas in which scale, proportion, and quantity can be used throughout their curriculum. Can you find another activity in the practices can be sharpened with the use of this CCC? Try to find one in another practice.
A tenth grader uses his testable question as the basis of an investigation and identifies proportions and quantity of populations to reach a conclusion.
A fifth grader explores Earth’s Place in the Universe (content) with developing and using models (practice) with a focus in Scale, Proportion, and Quantity (CCC).
Scale, Proportion & Quantity Progression through Gradebands:
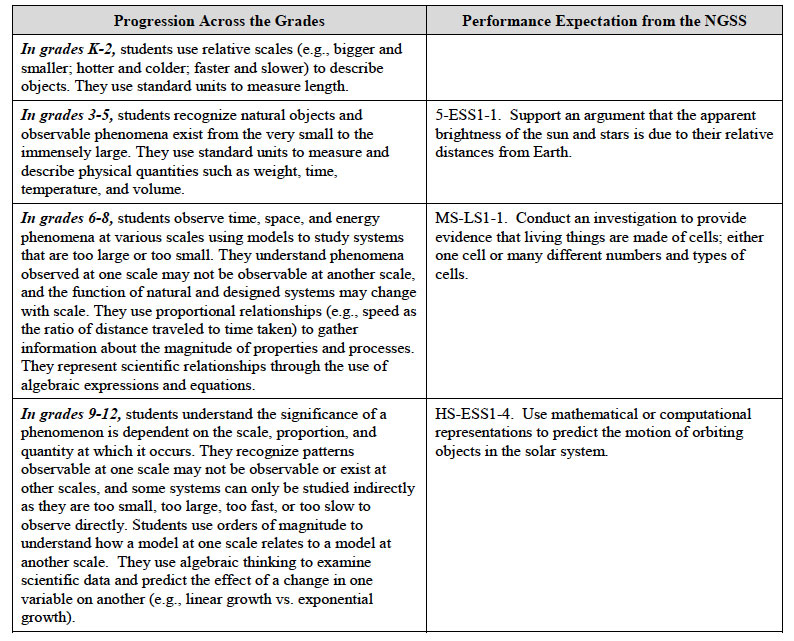
Progression from NGSS Appendix G p. 7
In the words of the Framework…
In thinking scientifically about systems and processes, it is essential to recognize that they vary in size (e.g., cells, whales, galaxies), in time span (e.g., nanoseconds, hours, millennia), in the amount of energy flowing through them (e.g., lightbulbs, power grids, the sun), and in the relationships between the scales of these different quantities. The understanding of relative magnitude is only a starting point. As noted in Benchmarks for Science Literacy, “The large idea is that the way in which things work may change with scale. Different aspects of nature change at different rates with changes in scale, and so the relationships among them change, too” [4]. Appropriate understanding of scale relationships is critical as well to engineering—no structure could be conceived, much less constructed, without the engineer’s precise sense of scale.
From a human perspective, one can separate three major scales at which to study science: (1) macroscopic scales that are directly observable—that is, what one can see, touch, feel, or manipulate; (2) scales that are too small or fast to observe directly; and (3) those that are too large or too slow. Objects at the atomic scale, for example, may be described with simple models, but the size of atoms and the number of atoms in a system involve magnitudes that are difficult to imagine. At the other extreme, science deals in scales that are equally difficult to imagine because they are so large—continents that move, for example, and galaxies in which the nearest star is 4 years away traveling at the speed of light. As size scales change, so do time scales. Thus, when considering large entities such as mountain ranges, one typically needs to consider change that occurs over long periods. Conversely, changes in a small-scale system, such as a cell, are viewed over much shorter times. However, it is important to recognize that processes that occur locally and on short time scales can have long-term and large-scale impacts as well.
In forming a concept of the very small and the very large, whether in space or time, it is important to have a sense not only of relative scale sizes but also of what concepts are meaningful at what scale. For example, the concept of solid matter is meaningless at the subatomic scale, and the concept that light takes time to travel a given distance becomes more important as one considers large distances across the universe.
Understanding scale requires some insight into measurement and an ability to think in terms of orders of magnitude—for example, to comprehend the difference between one in a hundred and a few parts per billion. At a basic level, in order to identify something as bigger or smaller than something else—and how much bigger or smaller—a student must appreciate the units used to measure it and develop a feel for quantity.
The ideas of ratio and proportionality as used in science can extend and challenge students’ mathematical understanding of these concepts. To appreciate the relative magnitude of some properties or processes, it may be necessary to grasp the relationships among different types of quantities—for example, speed as the ratio of distance traveled to time taken, density as a ratio of mass to volume. This use of ratio is quite different than a ratio of numbers describing fractions of a pie. Recognition of such relationships among different quantities is a key step in forming mathematical models that interpret scientific data.
Text from A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas