Adding the CCC to Your Curriculum
Cross-Cutting Concepts (CCC’s) lend a sharper focus to the other two dimensions. Each CCC presents a unique lens in which to focus upon the content while the practice provides the method in which the content is explored. The particular focus of “Systems and System Models” is best described in the words of the Framework below.
To begin the process of adding a cause and effect focus to your curriculum, begin with one activity or lesson. For example, Developing & Using Models Activity #1: Syringe and Plunger does not need to be altered in order to apply the third dimension of CCC’s. Drawing a system model for the phenomena sharpens the focus of the activity and provides touchstones for students throughout discourse. Framing questions around the model drawing will provide structure for discourse, notebooking, and student thinking. Students are exploring the syringe (content in this case) by way of developing and using models (practice). These questions are sharpened and focused through the lens of systems and system models (CCC). In this way, the activity has not been drastically altered. It has rather been more focused for both students and teachers in communication, analyzation, and discourse.
In this particular CCC, the modeling practice overlaps quite a bit. It can be difficult to separate the practice of models from the CCC of models. The key in applying the CCC is that the model is a system. Systems, whether closed or opened, behave by unique rules. Modeling does not always imitate a system. This is the technical, but key, difference between the practice and the CCC.
For instance, in Developing & Using Models Activity #2: Create Your Own Water Cycle the model focuses on modeling a system. Modeling a system focuses on interdependencies and interactions. Whereas, in Developing & Using Models Activity #3: Build-A-Bug the model focuses on the structure and function of the organism. Modeling structure and function focuses on particular features and their uses.
After initial implementation, instructors will be able to identify other areas in which system and system models can be used throughout their curriculum. Can you identify one unit in your curriculum that can be sharpened with the use of system and system models?
System and System Models Progression through Gradebands:
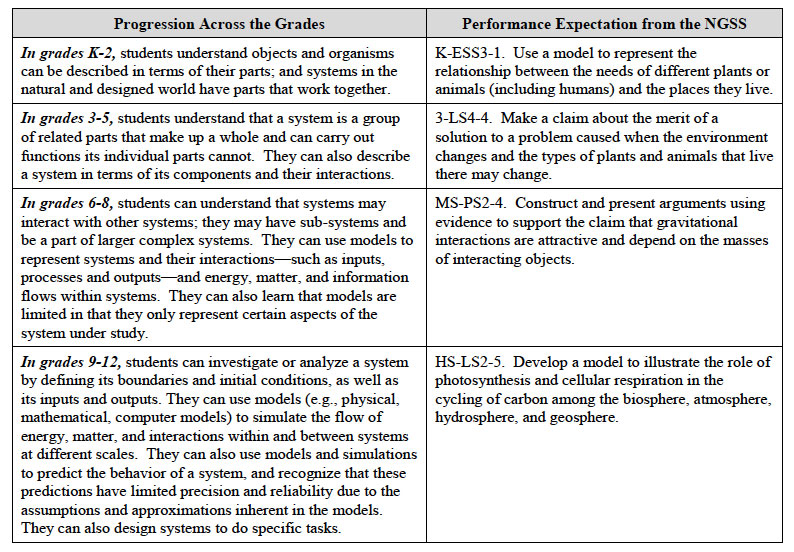
Progression from NGSS Appendix G p. 8
In the words of the Framework…
As noted in the National Science Education Standards, “The natural and designed world is complex; it is too large and complicated to investigate and comprehend all at once. Scientists and students learn to define small portions for the convenience of investigation. The units of investigations can be referred to as ‘systems.’ A system is an organized group of related objects or components that form a whole. Systems can consist, for example, of organisms, machines, fundamental particles, galaxies, ideas, and numbers. Systems have boundaries, components, resources, flow, and feedback” [2].
Although any real system smaller than the entire universe interacts with and is dependent on other (external) systems, it is often useful to conceptually isolate a single system for study. To do this, scientists and engineers imagine an artificial boundary between the system in question and everything else. They then examine the system in detail while treating the effects of things outside the boundary as either forces acting on the system or flows of matter and energy across it—for example, the gravitational force due to Earth on a book lying on a table or the carbon dioxide expelled by an organism. Consideration of flows into and out of the system is a crucial element of system design. In the laboratory or even in field research, the extent to which a system under study can be physically isolated or external conditions controlled is an important element of the design of an investigation and interpretation of results.
Often, the parts of a system are interdependent, and each one depends on or supports the functioning of the system’s other parts. Yet the properties and behavior of the whole system can be very different from those of any of its parts, and large systems may have emergent properties, such as the shape of a tree, that cannot be predicted in detail from knowledge about the components and their interactions. Things viewed as subsystems at one scale may themselves be viewed as whole systems at a smaller scale. For example, the circulatory system can be seen as an entity in itself or as a subsystem of the entire human body; a molecule can be studied as a stable configuration of atoms but also as a subsystem of a cell or a gas.
An explicit model of a system under study can be a useful tool not only for gaining understanding of the system but also for conveying it to others. Models of a system can range in complexity from lists and simple sketches to detailed computer simulations or functioning prototypes.
Models can be valuable in predicting a system’s behaviors or in diagnosing problems or failures in its functioning, regardless of what type of system is being examined. A good system model for use in developing scientific explanations or engineering designs must specify not only the parts, or subsystems, of the system but also how they interact with one another. It must also specify the boundary of the system being modeled, delineating what is included in the model and what is to be treated as external. In a simple mechanical system, interactions among the parts are describable in terms of forces among them that cause changes in motion or physical stresses. In more complex systems, it is not always possible or useful to consider interactions at this detailed mechanical level, yet it is equally important to ask what interactions are occurring (e.g., predator-prey relationships in an ecosystem) and to recognize that they all involve transfers of energy, matter, and (in some cases) information among parts of the system.
Any model of a system incorporates assumptions and approximations; the key is to be aware of what they are and how they affect the model’s reliability and precision. Predictions may be reliable but not precise or, worse, precise but not reliable; the degree of reliability and precision needed depends on the use to which the model will be put.
Text from A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas


