Adding the CCC to Your Curriculum
Cross-Cutting Concepts (CCC’s) lend a sharper focus to the other two dimensions. Each CCC presents a unique lens in which to focus upon the content while the practice provides the method in which the content is explored. The particular focus of “Stability and Change” is best described in the words of the Framework below.
To begin the process of adding a stability and change focus to your curriculum, begin with one activity or lesson. For instance, Developing & Using Models Activity #5: Measuring Albedo and Climate Modeling does not need to be altered in order to apply the third dimension of CCC’s. How can Stability and Change be used to sharpen this activity? How would you focus on the CCC? How would your students focus on the CCC?

Tenth grade student uses a testable question to design an investigation. Could this project be focused on the CCC of Stability and Change? What questions could be framed around Stability and Change?
Stability and Change Progression through Gradebands:
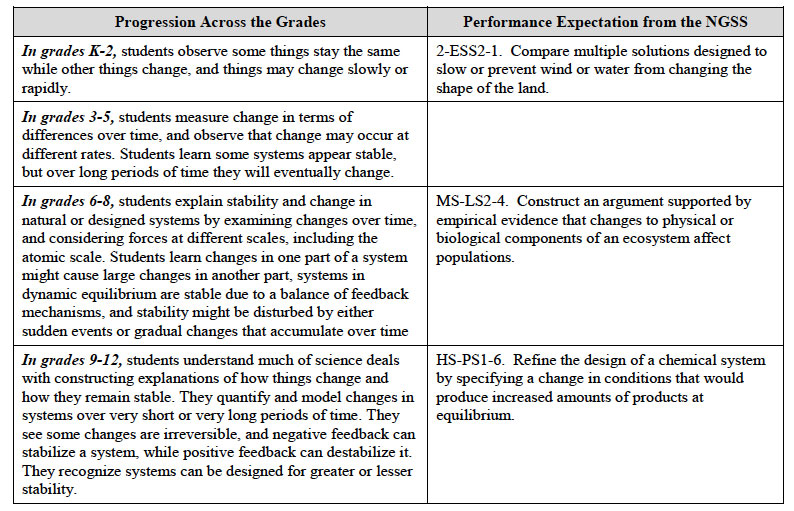
Progression from NGSS Appendix G p. 11
In the words of the Framework…
Much of science and mathematics has to do with understanding how change occurs in nature and in social and technological systems, and much of technology has to do with creating and controlling change,” according to the American Association for the Advancement of Science. “Constancy, often in the midst of change, is also the subject of intense study in science” [4].
Stability denotes a condition in which some aspects of a system are unchanging, at least at the scale of observation. Stability means that a small disturbance will fade away—that is, the system will stay in, or return to, the stable condition. Such stability can take different forms, with the simplest being a static equilibrium, such as a ladder leaning on a wall. By contrast, a system with steady inflows and outflows (i.e., constant conditions) is said to be in dynamic equilibrium. For example, a dam may be at a constant level with steady quantities of water coming in and out. Increase the inflow, and a new equilibrium level will eventually be reached if the outflow increases as well. At extreme flows, other factors may cause disequilibrium; for example, at a low-enough inflow, evaporation may cause the level of the water to continually drop. Likewise, a fluid at a constant temperature can be in a steady state with constant chemical composition even though chemical reactions that change the composition in two opposite directions are occurring within it; change the temperature and it will reach a new steady state with a different composition.
A repeating pattern of cyclic change—such as the moon orbiting Earth—can also be seen as a stable situation, even though it is clearly not static. Such a system has constant aspects, however, such as the distance from Earth to the moon, the period of its orbit, and the pattern of phases seen over time.
In designing systems for stable operation, the mechanisms of external controls and internal “feedback” loops are important design elements; feedback is important to understanding natural systems as well. A feedback loop is any mechanism in which a condition triggers some action that causes a change in that same condition, such as the temperature of a room triggering the thermostatic control that turns the room’s heater on or off. Feedback can stabilize a system (negative feedback—a thermostat in a cooling room triggers heating, but only until a particular temperature range is reached) or destabilize a system (positive feedback—a fire releases heat, which triggers the burning of more fuel, which causes the fire to continue to grow).
A system can be stable on a small time scale, but on a larger time scale it may be seen to be changing. For example, when looking at a living organism over the course of an hour or a day, it may maintain stability; over longer periods, the organism grows, ages, and eventually dies. For the development of larger systems, such as the variety of living species inhabiting Earth or the formation of a galaxy, the relevant time scales may be very long indeed; such processes occur over millions or even billions of years.
When studying a system’s patterns of change over time, it is also important to examine what is unchanging. Understanding the feedback mechanisms that regulate the system’s stability or that drive its instability provides insight into how the system may operate under various conditions. These mechanisms are important to evaluate when comparing different design options that address a particular problem.
Any system has a range of conditions under which it can operate in a stable fashion, as well as conditions under which it cannot function. For example, a particular living organism can survive only within a certain range of temperatures, and outside that span it will die. Thus elucidating what range of conditions can lead to a system’s stable operation and what changes would destabilize it (and in what ways) is an important goal.
Note that stability is always a balance of competing effects; a small change in conditions or in a single component of the system can lead to runaway changes in the system if compensatory mechanisms are absent. Nevertheless, students typically begin with an idea of equilibrium as a static situation, and they interpret a lack of change in the system as an indication that nothing is happening. Thus they need guidance to begin to appreciate that stability can be the result of multiple opposing forces; they should be taught to identify the invisible forces—to appreciate the dynamic equilibrium—in a seemingly static situation, even one as simple as a book lying on a table.
An understanding of dynamic equilibrium is crucial to understanding the major issues in any complex system—for example, population dynamics in an ecosystem or the relationship between the level of atmospheric carbon dioxide and Earth’s average temperature. Dynamic equilibrium is an equally important concept for understanding the physical forces in matter. Stable matter is a system of atoms in dynamic equilibrium.
For example, the stability of the book lying on the table depends on the fact that minute distortions of the table caused by the book’s downward push on the table in turn cause changes in the positions of the table’s atoms. These changes then alter the forces between those atoms, which lead to changes in the upward force on the book exerted by the table. The book continues to distort the table until the table’s upward force on the book exactly balances the downward pull of gravity on the book. Place a heavy enough item on the table, however, and stability is not possible; the distortions of matter within the table continue to the macroscopic scale, and it collapses under the weight. Such seemingly simple, explicit, and visible examples of how change in some factor produces changes in the system can help to establish a mental model of dynamic equilibrium useful for thinking about more complex systems.
Understanding long-term changes—for example, the evolution of the diversity of species, the surface of Earth, or the structure of the universe—requires a sense of the requisite time scales for such changes to develop. Long time scales can be difficult for students to grasp, however. Part of their understanding should grow from an appreciation of how scientists investigate the nature of these processes—through the interplay of evidence and system modeling. Studentdeveloped models that use comparative time scales can also be helpful; for example, if the history of Earth is scaled to 1 year (instead of the absolute measures in eons), students gain a more intuitive understanding of the relative durations of periods in the planet’s evolution.
Text from A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas


